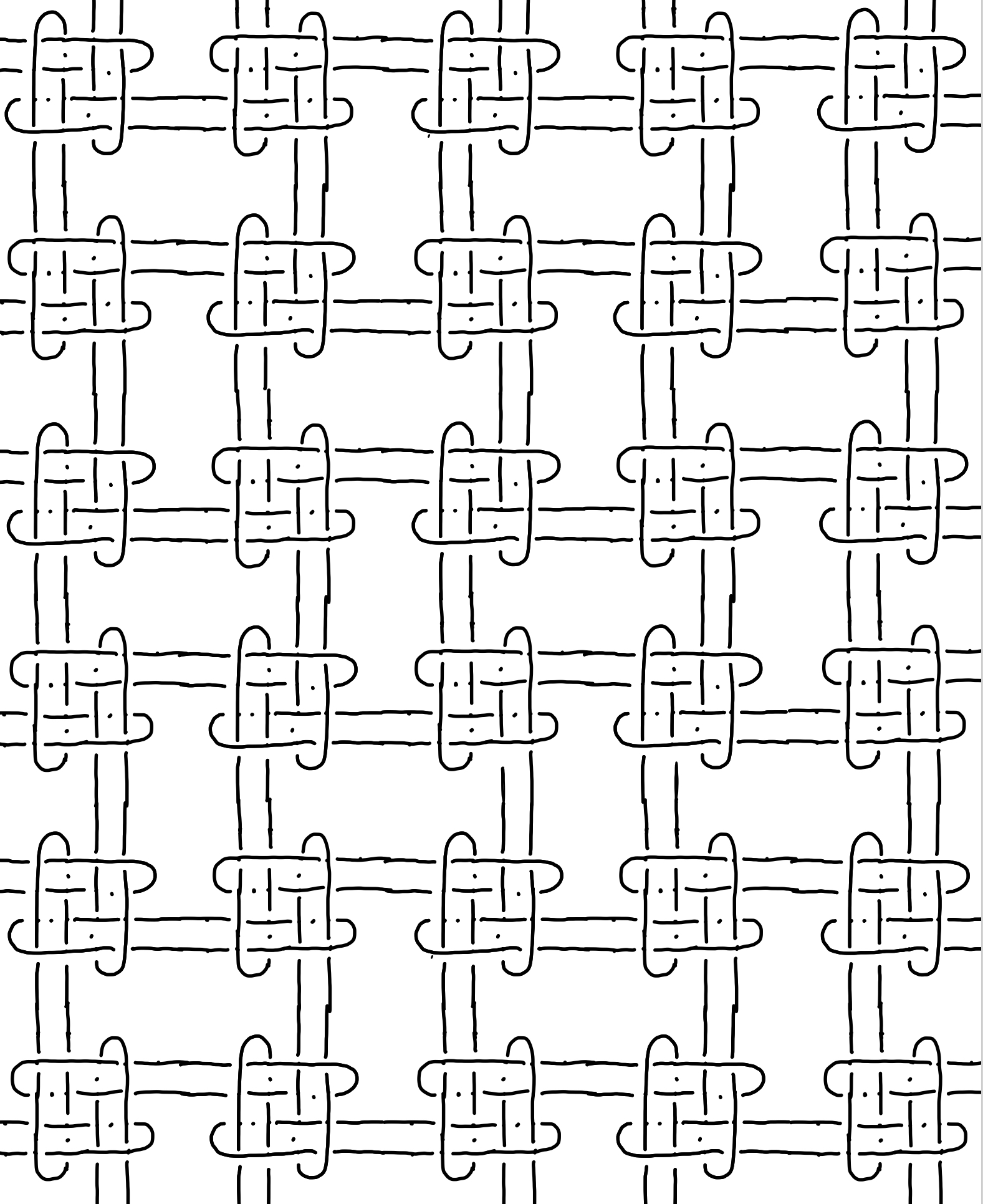
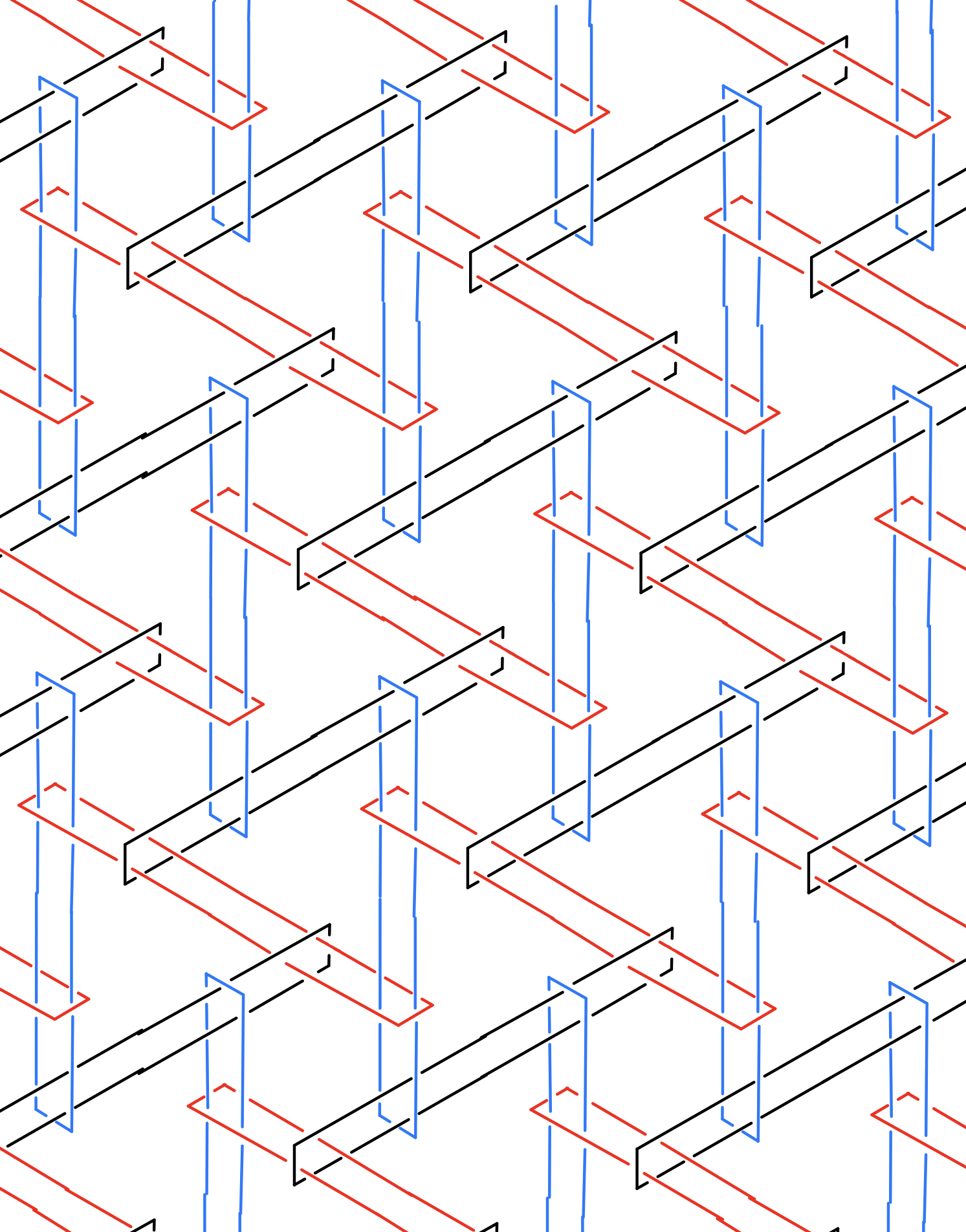
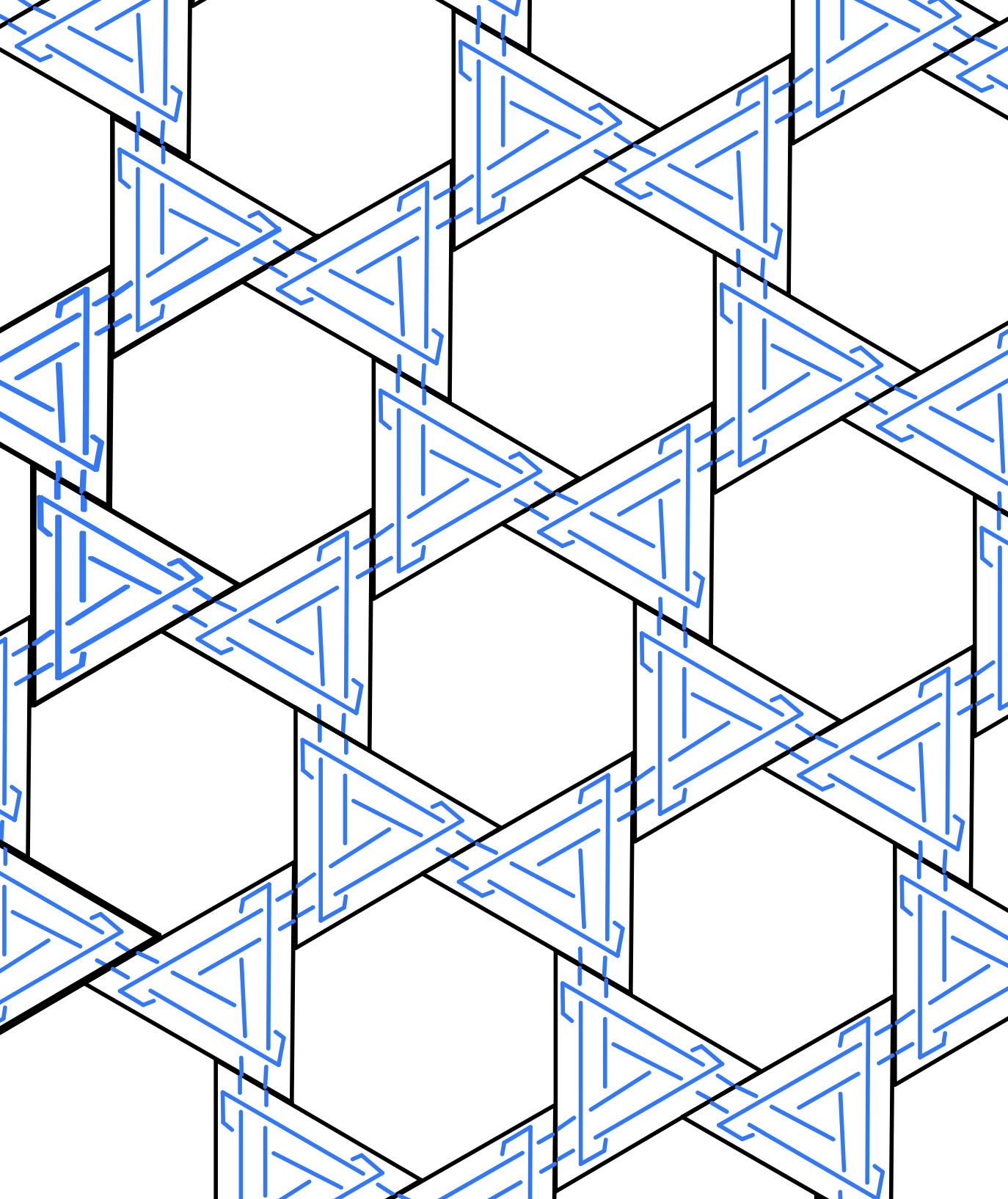
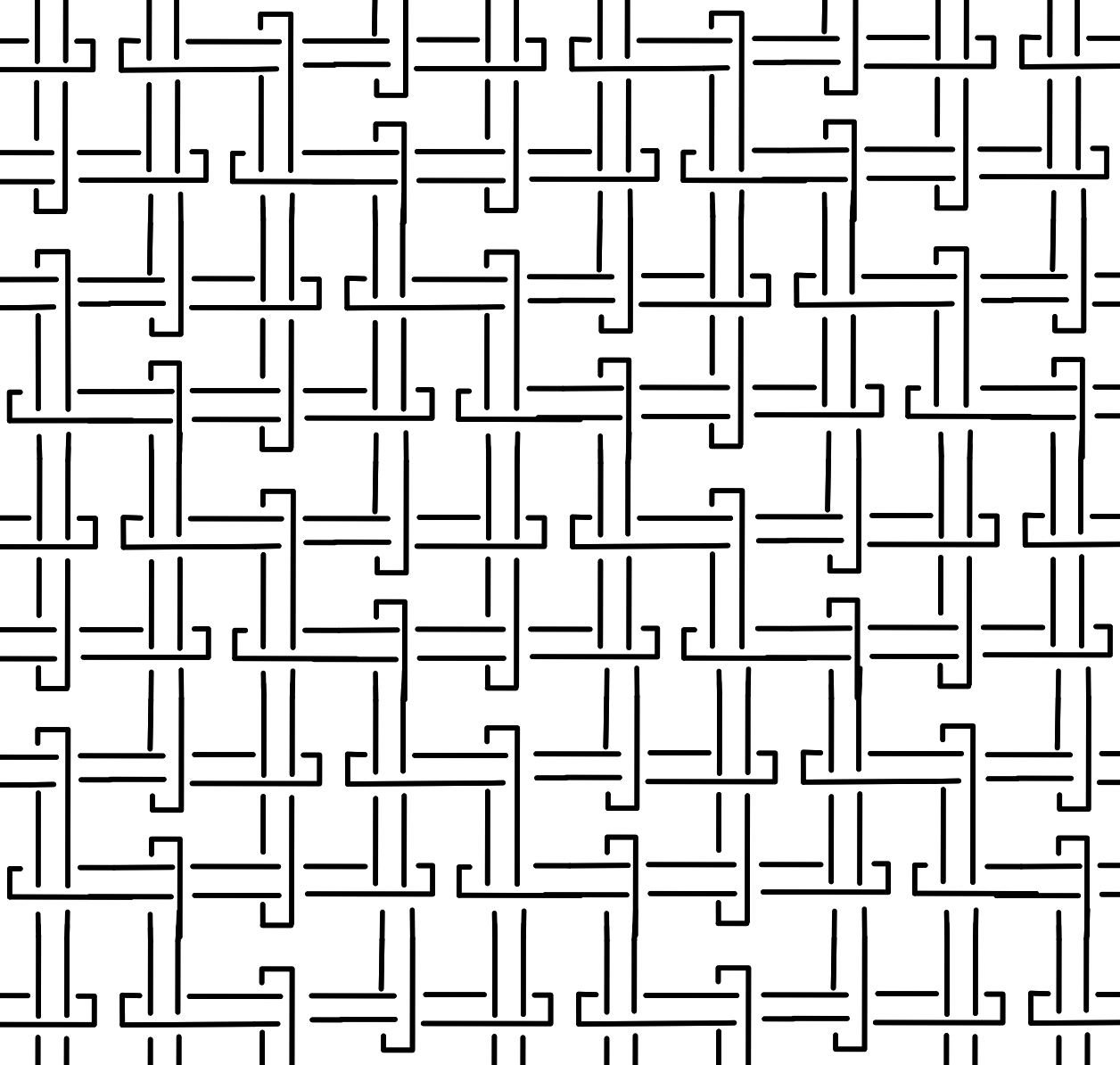
I've always been fascinated by Brunnian links. They have the peculiar property of falling apart if any individual component is removed. As such, they are a wonderful metaphor for the complex, fragile connections that keep this world together. The above picture shows lasercut tiles that assemble into Brunnian links, hence I called them "ti-links". Any polyhedron or tiling can be transformed into a Brunnain Link using this (after stretching if the polygons are irregular). I developed this system in a short paper for the 2024 Bridges Math Art Conference. Essentially, modules with a swirl of k bands are in bijection with vertices of degree k in a graph, so actually, this system allows one to translate any graph into a Brunnian link! More details, and other associate crafts, are described on the page for an outreach activity I did for this. 
