 Temari are emrbroidered balls, a traditional Japanese handicraft. Each one starts as a styrofoam ball (or rolled scraps of fabric), which is wrapped in yarn then thread, and finally embroidered with a pattern. In addition to being quite stunning, they are a great way to play around with spherical symmetries.
Temari are emrbroidered balls, a traditional Japanese handicraft. Each one starts as a styrofoam ball (or rolled scraps of fabric), which is wrapped in yarn then thread, and finally embroidered with a pattern. In addition to being quite stunning, they are a great way to play around with spherical symmetries.  This ball features an "orderly tangle", a link with polygonal components. There are some great models of these by George Hart and also discussed in a book by Alan Holden. I've found making models with plastic straws put end-into-end to form triangles and square is a good way to play around with these. This design uses the duality of the color scheme, black and white, to draw attention to the dual nature of the octahedron and cube: every vertex of one corresponds to a face of the other.
This ball features an "orderly tangle", a link with polygonal components. There are some great models of these by George Hart and also discussed in a book by Alan Holden. I've found making models with plastic straws put end-into-end to form triangles and square is a good way to play around with these. This design uses the duality of the color scheme, black and white, to draw attention to the dual nature of the octahedron and cube: every vertex of one corresponds to a face of the other.  The pair shows more orderly tangles. The pink and blue color scheme is inverted between the two, as each represent different ways of interleaving six squares, one for each vertex of an octahedron. The pink base has the sqaures in the orientation of a cube, whereas the blue base has them rotated 45 degrees. Both designs are overlaid with a tangle of eight triangles, colored yellow and white to represent the two tetrahedra of a stella octangula. Despite looking different, they are the same confinguration in each.
The pair shows more orderly tangles. The pink and blue color scheme is inverted between the two, as each represent different ways of interleaving six squares, one for each vertex of an octahedron. The pink base has the sqaures in the orientation of a cube, whereas the blue base has them rotated 45 degrees. Both designs are overlaid with a tangle of eight triangles, colored yellow and white to represent the two tetrahedra of a stella octangula. Despite looking different, they are the same confinguration in each. 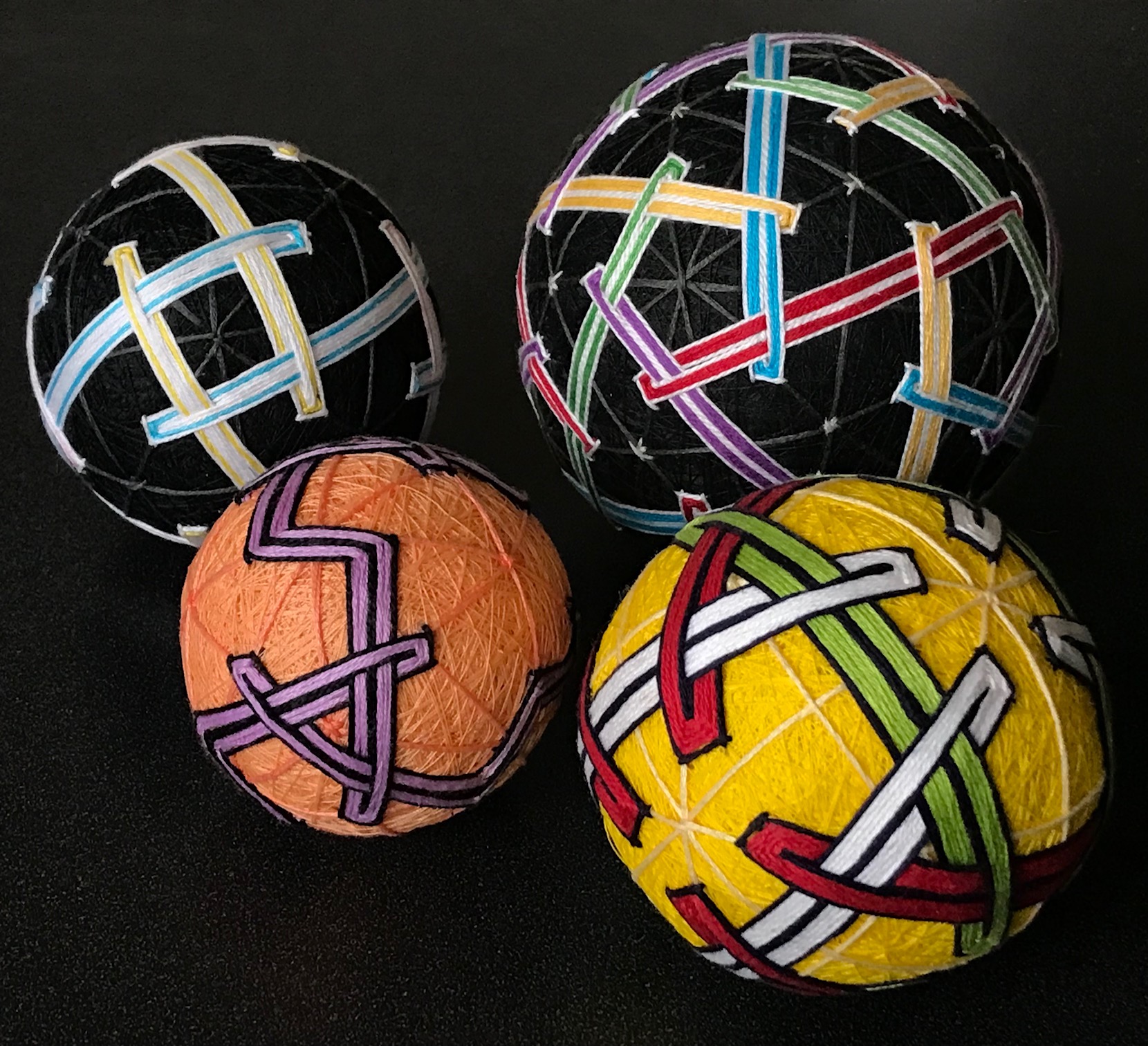 These temari are based on a system of generating Brunnian Links I developped and presented at the 2024 Bridge's conference with a short paper and outreach activity. These designs are based on polyhedra, where each face is decorated with a module, combining to form the link. The yellow has a swirl of three bands for each face of an octahedron, with mirrors along three planes. The orange ball has tetrahedral symmetry. The smaller black ball has a swirl of four bands for each face of the cube. The larger black ball has a module for each face of the dodecahedron. I've also color coded the bands to help evoke the underlying symmetry, for example the dodecahedral design is based on an edge coloring of the dodechedral graph.
These temari are based on a system of generating Brunnian Links I developped and presented at the 2024 Bridge's conference with a short paper and outreach activity. These designs are based on polyhedra, where each face is decorated with a module, combining to form the link. The yellow has a swirl of three bands for each face of an octahedron, with mirrors along three planes. The orange ball has tetrahedral symmetry. The smaller black ball has a swirl of four bands for each face of the cube. The larger black ball has a module for each face of the dodecahedron. I've also color coded the bands to help evoke the underlying symmetry, for example the dodecahedral design is based on an edge coloring of the dodechedral graph.  Temari are emrbroidered balls, a traditional Japanese handicraft. Each one starts as a styrofoam ball (or rolled scraps of fabric), which is wrapped in yarn then thread, and finally embroidered with a pattern. In addition to being quite stunning, they are a great way to play around with spherical symmetries.
Temari are emrbroidered balls, a traditional Japanese handicraft. Each one starts as a styrofoam ball (or rolled scraps of fabric), which is wrapped in yarn then thread, and finally embroidered with a pattern. In addition to being quite stunning, they are a great way to play around with spherical symmetries.  This ball features an "orderly tangle", a link with polygonal components. There are some great models of these by George Hart and also discussed in a book by Alan Holden. I've found making models with plastic straws put end-into-end to form triangles and square is a good way to play around with these. This design uses the duality of the color scheme, black and white, to draw attention to the dual nature of the octahedron and cube: every vertex of one corresponds to a face of the other.
This ball features an "orderly tangle", a link with polygonal components. There are some great models of these by George Hart and also discussed in a book by Alan Holden. I've found making models with plastic straws put end-into-end to form triangles and square is a good way to play around with these. This design uses the duality of the color scheme, black and white, to draw attention to the dual nature of the octahedron and cube: every vertex of one corresponds to a face of the other.  The pair shows more orderly tangles. The pink and blue color scheme is inverted between the two, as each represent different ways of interleaving six squares, one for each vertex of an octahedron. The pink base has the sqaures in the orientation of a cube, whereas the blue base has them rotated 45 degrees. Both designs are overlaid with a tangle of eight triangles, colored yellow and white to represent the two tetrahedra of a stella octangula. Despite looking different, they are the same confinguration in each.
The pair shows more orderly tangles. The pink and blue color scheme is inverted between the two, as each represent different ways of interleaving six squares, one for each vertex of an octahedron. The pink base has the sqaures in the orientation of a cube, whereas the blue base has them rotated 45 degrees. Both designs are overlaid with a tangle of eight triangles, colored yellow and white to represent the two tetrahedra of a stella octangula. Despite looking different, they are the same confinguration in each. 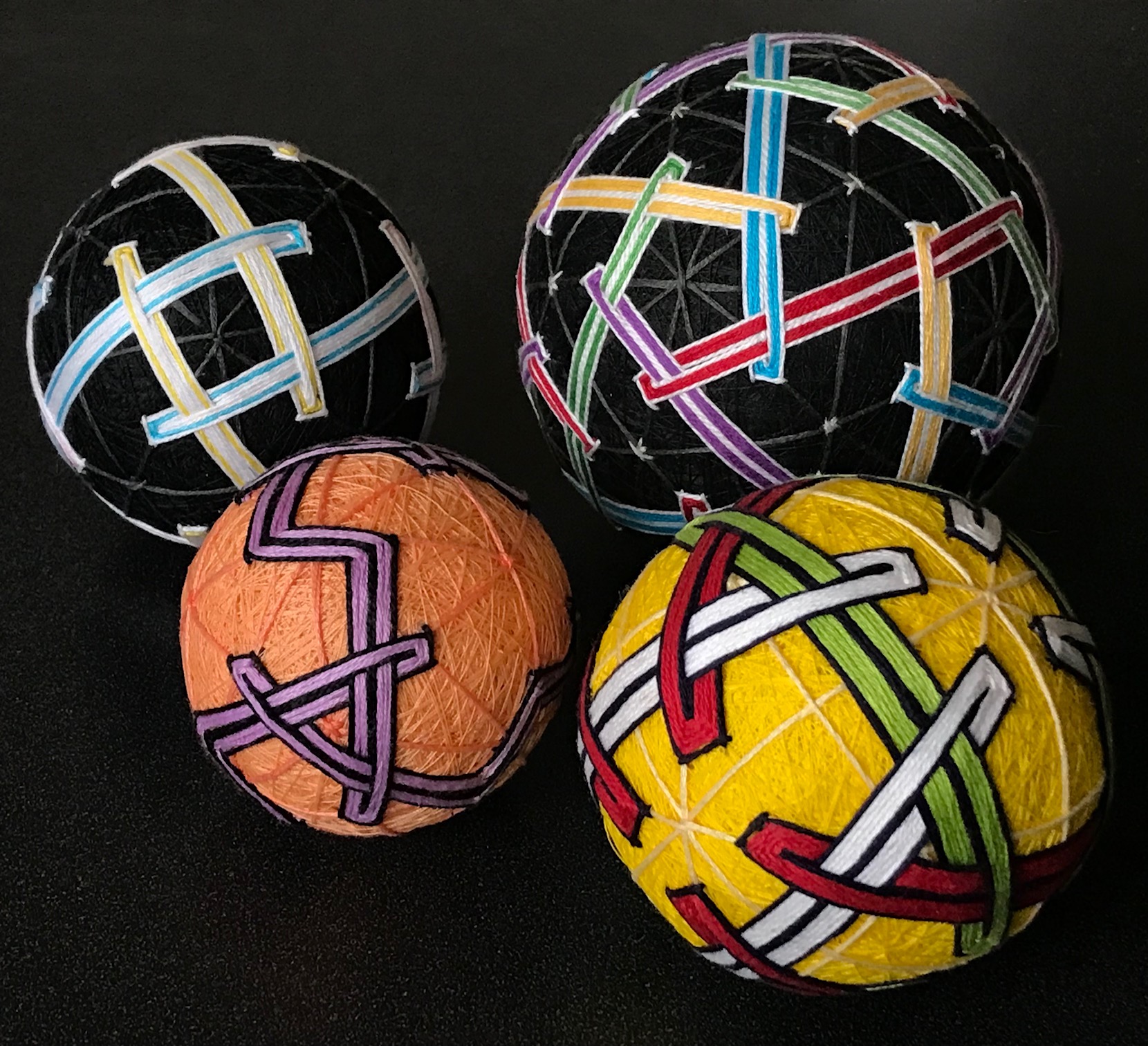 These temari are based on a system of generating Brunnian Links I developped and presented at the 2024 Bridge's conference with a short paper and outreach activity. These designs are based on polyhedra, where each face is decorated with a module, combining to form the link. The yellow has a swirl of three bands for each face of an octahedron, with mirrors along three planes. The orange ball has tetrahedral symmetry. The smaller black ball has a swirl of four bands for each face of the cube. The larger black ball has a module for each face of the dodecahedron. I've also color coded the bands to help evoke the underlying symmetry, for example the dodecahedral design is based on an edge coloring of the dodechedral graph.
These temari are based on a system of generating Brunnian Links I developped and presented at the 2024 Bridge's conference with a short paper and outreach activity. These designs are based on polyhedra, where each face is decorated with a module, combining to form the link. The yellow has a swirl of three bands for each face of an octahedron, with mirrors along three planes. The orange ball has tetrahedral symmetry. The smaller black ball has a swirl of four bands for each face of the cube. The larger black ball has a module for each face of the dodecahedron. I've also color coded the bands to help evoke the underlying symmetry, for example the dodecahedral design is based on an edge coloring of the dodechedral graph.