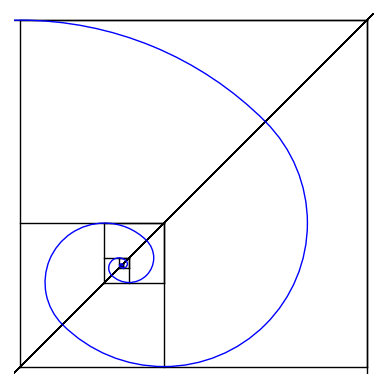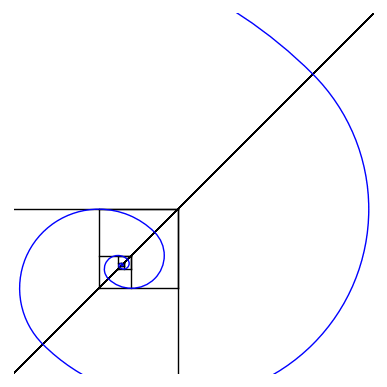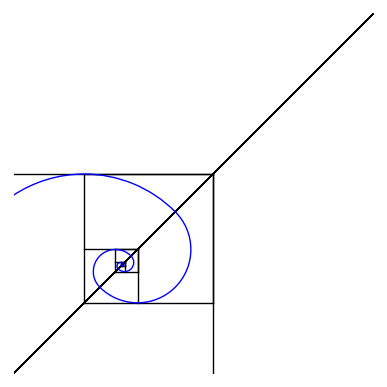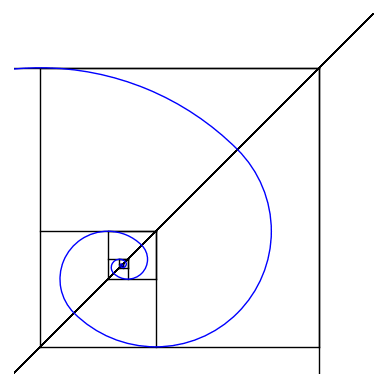
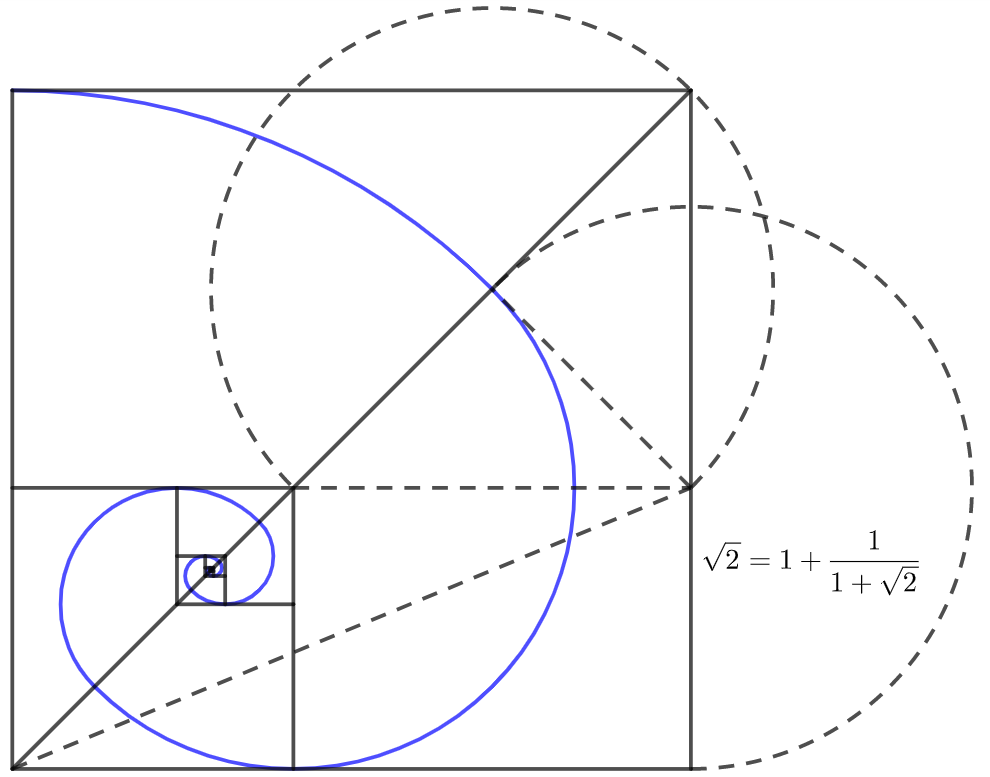
This Gif represents a "proof" that the square root of 2 is irrational. It is a geometric depiction of the fact that the continued fraction for sqrt(2) is 1/(2+1/(2+1/(2+...))), since x = sqrt(2) satisfies x = 1+1/(1+x). Like a fractal gif, the nesting of this represents a self-symmetry in the continued fraction. Since it never terminates, sqrt(2) is not rational. One can think of this as extending Euclid's division algorithm, using each remainder to divide the next, 1 goes into sqrt(2) once, then the remainder sqrt(2)-1 goes into 1 twice, and so on. I developed this during my time at the SMALL REU in William's College in the summer 2019 as part of a group project on continued fractions with Professor Thomas Garrity.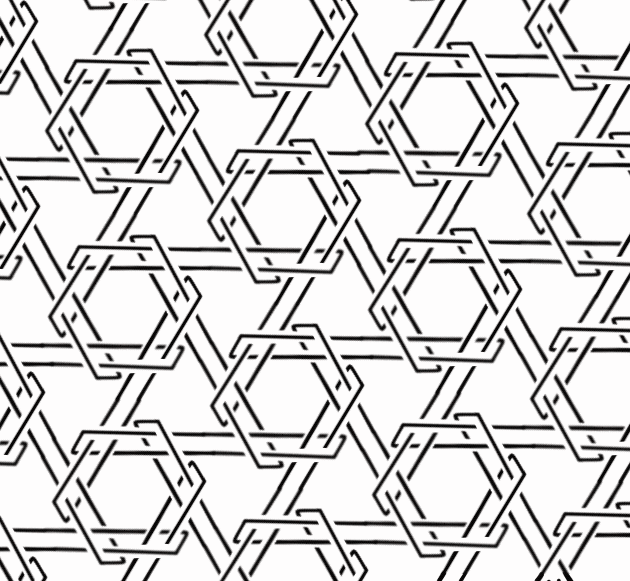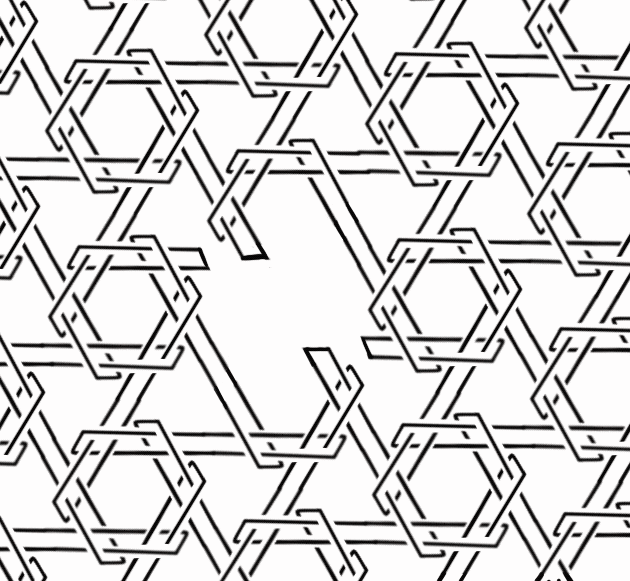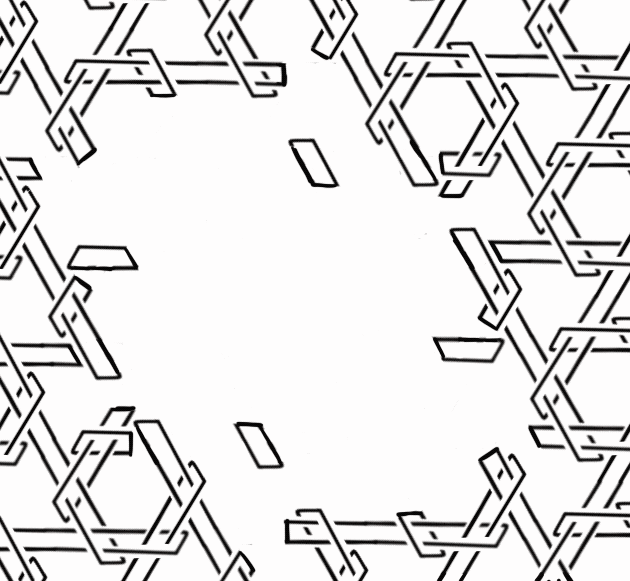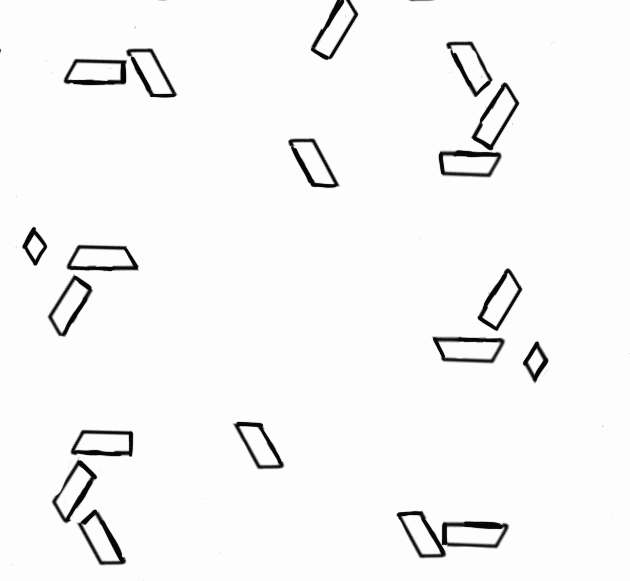 
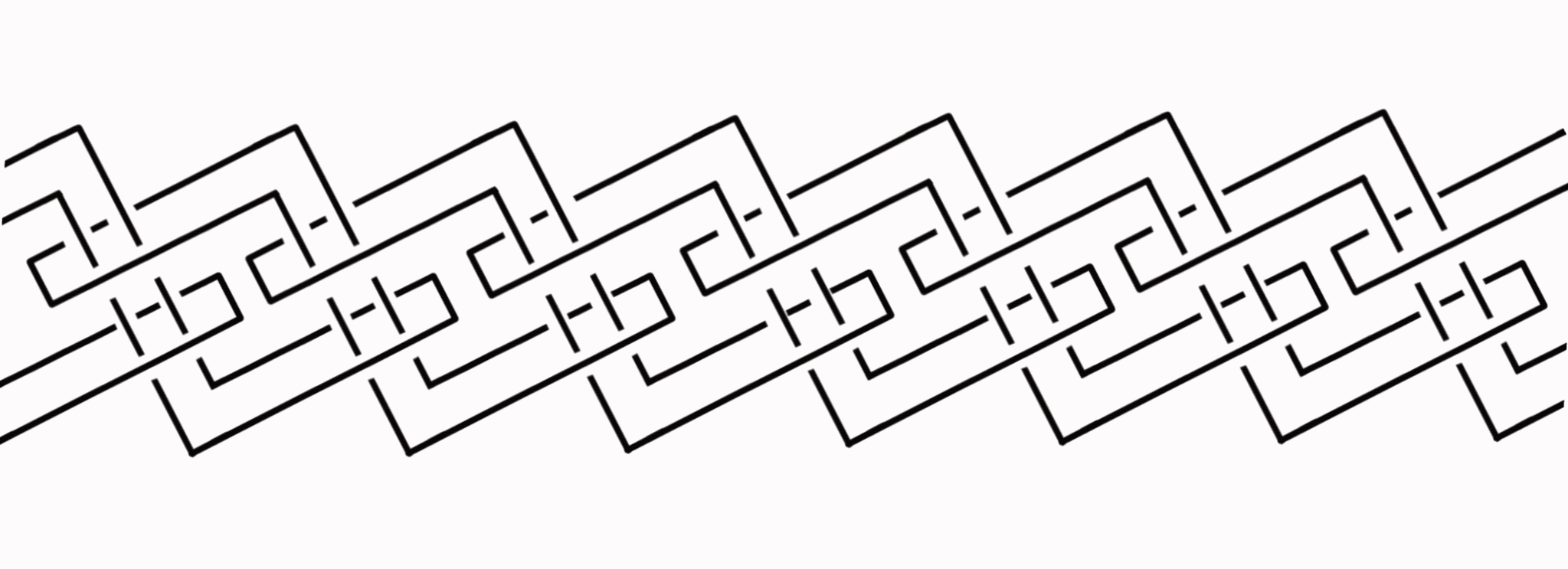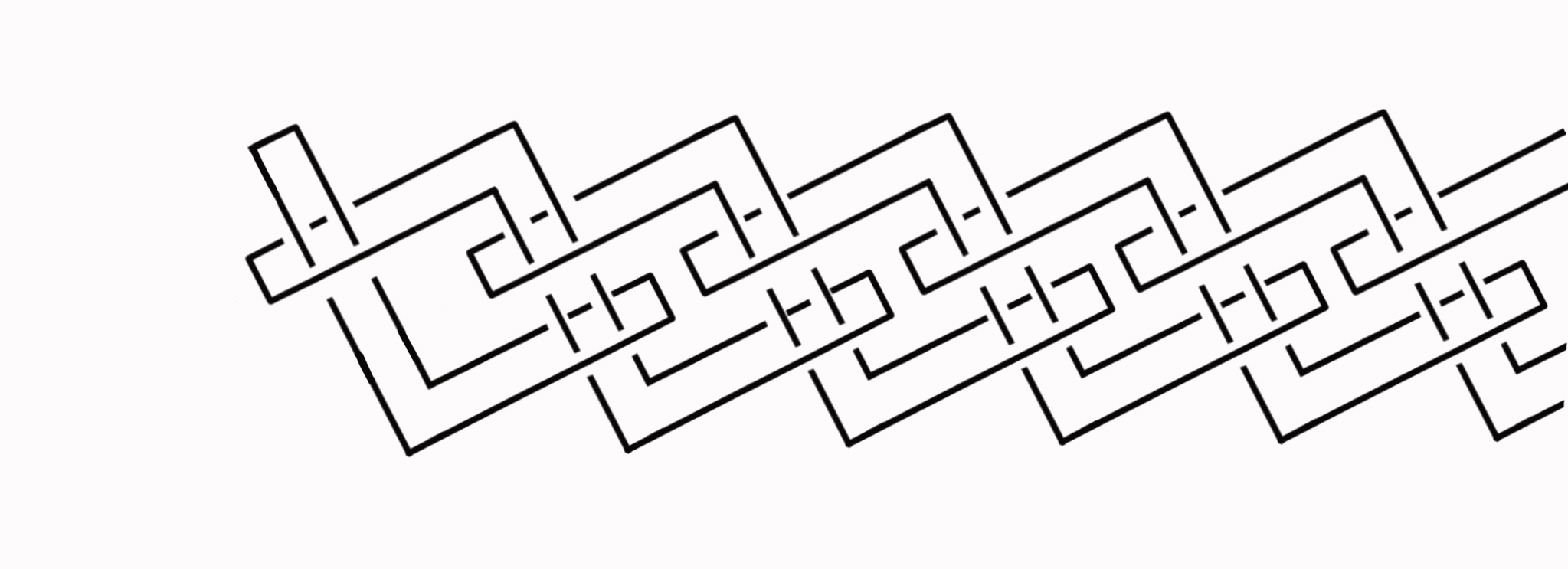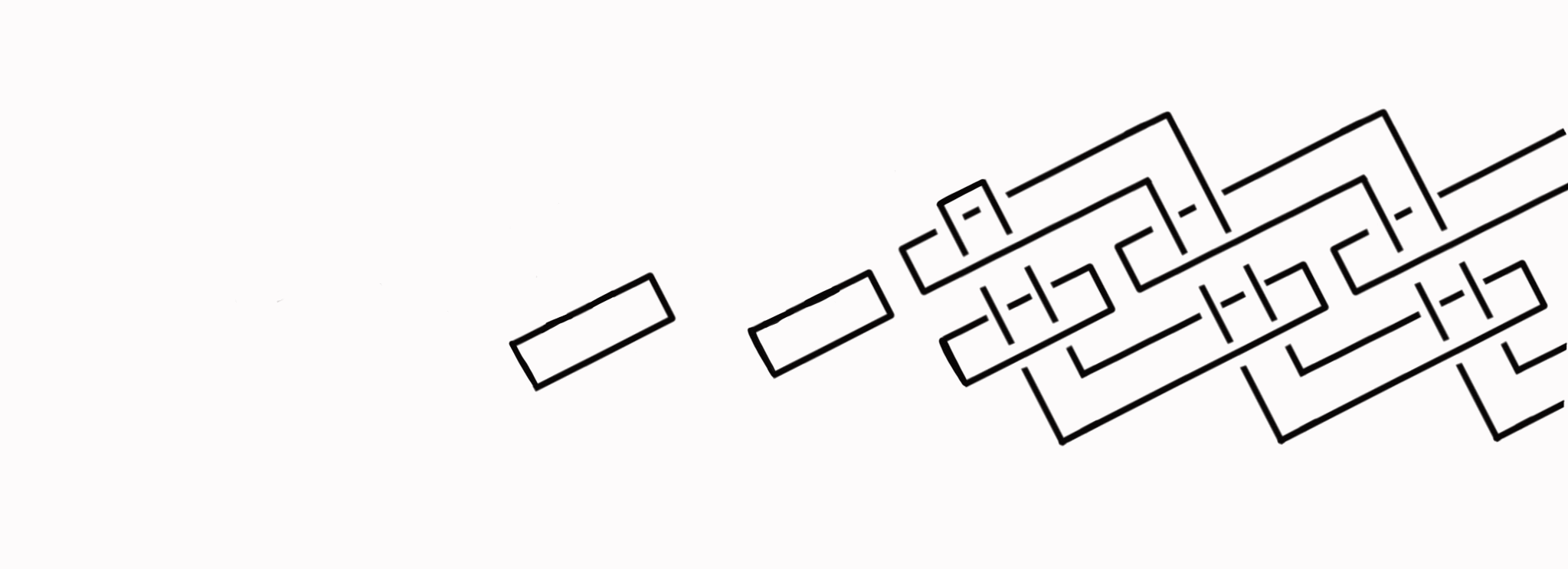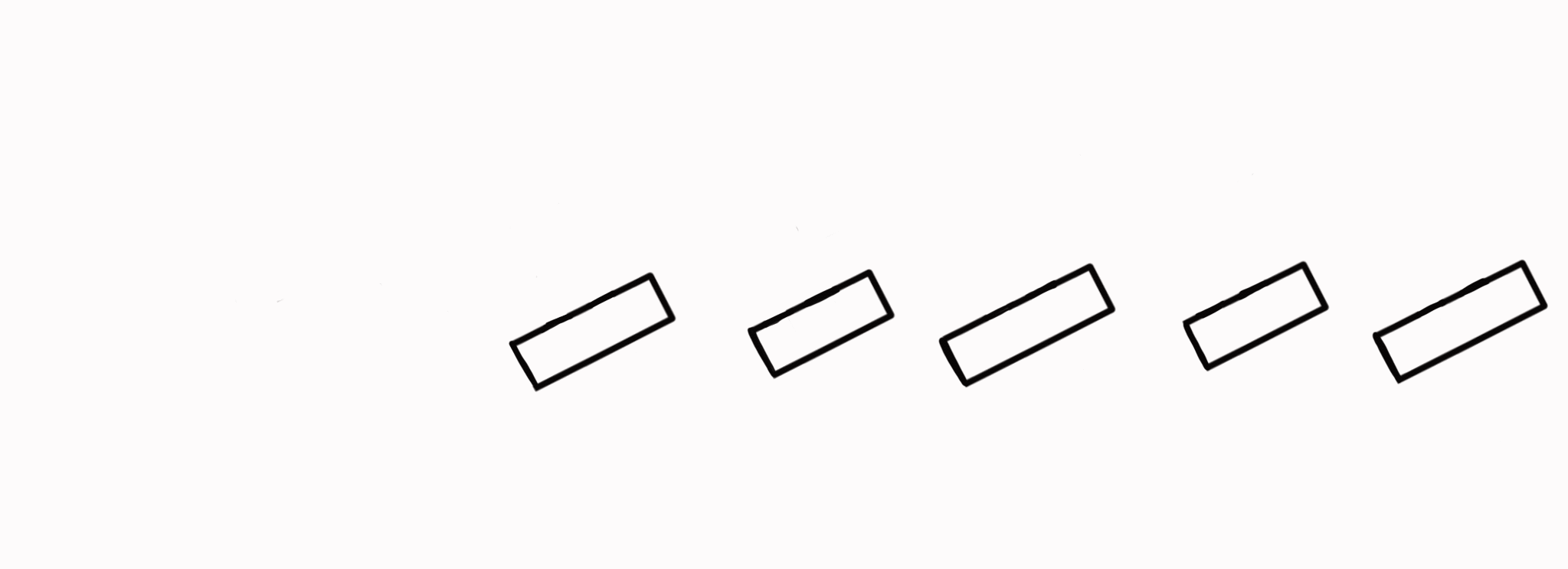The above shows a ti-link being unraveled. These are part of a modular system of generating Brunnian links described further at the preceding link. 